The questions in The Highway to Olympia are extraordinarily attention-grabbing, various on all subjects. This mental program is more and more with the extent of questions rising after every examination. A query within the Highway to Mount Olympia 17, February, and Quarter III has content material that many individuals are occupied with. The content material of the Olympia query is as follows: From the digits 1, 2, 3, what number of 3-digit numbers will be fashioned which might be divisible by 3?

After saying the query, many Japanese folks take into account this to be a simple query as a result of candidates solely must know the rule of numbers divisible by 3 to have the ability to rapidly discover the answer. Nevertheless, the contestant who pressed the bell gained the proper to reply and gave the fallacious reply. The proper reply to this query is 9 numbers.

To resolve the Olympia query, we simply want to use the rule: Numbers whose sum of digits is divisible by 3 is divisible by 3 and solely these numbers are divisible by 3. During which, the sum of three 1s, 2, 3 is 6 divisible by 3. So simply type three-digit numbers from these 3 numbers to search out the reply. The numbers created from the #1, 2, 3 which might be divisible by 3 are: 111, 222, 333, 123, 132, 213, 231, 312, 313.

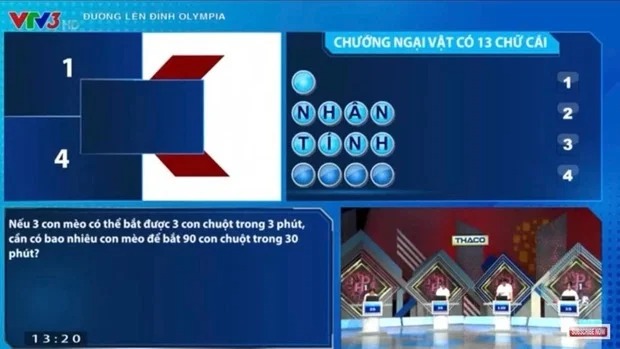
Beforehand, within the twenty second season, Highway to Olympia, the Impediment part of the primary episode of Q3 had the query: “If 3 cats can catch 3 mice in 3 minutes, what number of cats will it take to catch 90 mice in half-hour?”

This query makes it unimaginable for the candidate to present the right reply. The reply to the above downside is 9 cats.

Picture: Highway to Mount Olympia